Neural Systems
CNL Research
Flash-lag Effect
We previously showed that the flash-lag effect could be explained as a spatial bias caused by motion signals rather than time delays (Eagleman and Sejnowski 2000). We analyzed several other motion illusions and showed that spatial bias in localization judgments gives a unified explanation for the flash-lag, flash-drag, flash-jump and Frohlich illusions (Eagleman and Sejnowski 2007). In another study, early, cross modal interactions in the visual and auditory cortex assessed with event-related potentials underlie a sound-induced visual illusion (Mishra, Fellous et al. 2006). These studies point toward a window of 80 ms within which interactions between signals in the cortex can influence perceptual and timing judgments. Spatial interactions within the visual cortex can also alter perceptual judgments and we developed a cortical model in which the tilt illusion can be accounted for by changes in a system of divisive gain normalization (Schwartz, Sejnowski et al. 2009) whose function is to create a generative model of natural scene statistics (Schwartz, Sejnowski et al. 2006).
Priming
Prior exposure to an image improves subsequent responses and is accompanied by reduced neural activity. But whether suppression of neuronal activity with priming is responsible for the improvement in perception is unclear. In a model of visual cortex, we showed that perceptual priming could be explained by representation sharpening, in which connection strengths between neurons at a high firing rate were increased and connection strengths to low and moderately firing neurons decreased (Moldakarimov, Bazhenov et al. 2010). This led to decreased interference of representations in higher visual areas and faster recognition. The model explained a wide range of psychophysical and physiological data observed in priming experiments, including antipriming phenomena and a decrease of power in the gamma band. This produced sparse cortical codes for representing objects. Odor learning in insects may also depend on learning mechanisms that produce a sparse output representation. Building on previous models of the insect antennal lobe (Bazhenov, Stopfer et al. 2001; Bazhenov, Stopfer et al. 2001), activity-dependent plasticity at synapses from the antennal lobe drove the observed specificity, reliability, and expected persistence of odor representations in the mushroom bodies (Finelli, Haney et al. 2008)
Probabilistic Learning
Learning to associate visual features with probabilistic rewards involves the areas of the visual system interacting with other areas that predict future reward. We asked subjects to choose between visual features to decide on how to categorize an object and found that they chose features that optimize the information gain (Nelson, McKenzie et al. 2010). In an fMRI experiment, subjects presented with the more-useful feature produced higher activity than the less-useful feature in the ventral striatum (nucleus accumbens), amygdala/hippocampus, and cerebellar vermis (Filimon 2011). In a related probabilistic reward experiment, we showed that changes in the pattern of event-related potentials in the frontal cortex were consistent with reward prediction error (Peterson, Lotz et al. 2011) and Parkinson’s patients off medication had impaired reversal learning, suggesting that the dopamine reward system was involved.
Visual Search
Bottom up processing of visual input is combined with top down control in visual search tasks. We have developed a new search task in which observers quickly learn to find hidden targets on a blank screen, which are chosen on each trail from a Gaussian distribution (Chukoskie 2005). We showed that asymptotic subject performance matches the theoretical optimum for this task. This new task allows us to examine the top down signals in the brain without interference from bottom up visual processing. We are developing a temporal-difference reinforcement learning model to compare with human performance and to make predictions for where in the brain to look for the top down signals and changes during learning. We plan to study activity in the human cortex during this task with fMRI. The task is also rapidly acquired by monkeys and we will collaborate with Tom Albright at the Salk Institute to record from neurons in the parietal cortex of monkeys. Finally, we are collaborating with Andrea Chiba at UCSD to develop a rodent version of this search task (Alexander 2010).
Visuomotor Adaptation
When there is a rotation of the visual field relative to the body, the initial pointing error of the arm is compensated over time by adaptation, which is restricted to a narrow range of directions around the training direction. We developed a population-coding model that updated the weights between narrow Gaussian-tuned visual units and motor units on each trial. The model reproduced experimental trial-by-trial learning curves for rotation adaptation and the generalization function measured postadaptation, suggesting that rotation adaptation occurs at synapses between neurons in posterior parietal cortex and motor cortex driven by a prediction error computed by the cerebellum (Tanaka, Sejnowski et al. 2009). We also developed a multi-rate model of adaptation that has a fast, trial-by-trial component and a slower component that matched the psychophysical data (Tanaka in press).
Motor Cortex
There has been a long-standing disagreement between researchers about how neurons in the primary motor cortex control arm movements. Neurons have been found in motor cortex that compute joint torques and muscle tensions, but other motor cortex neurons carry kinematic spatial information and encode hand-movement directions and velocities. This has led to an impasse since motor cortex neuronal activities reflect such a broad mixture of movement-related variables, without explaining how a desired trajectory is converted by motor cortex neurons into joint torques. We have shown that the equations of motion for reaching based on the spatial positions of limbs in Cartesian coordinates are considerably more concise and have physically intuitive interpretations (Tanaka Submitted). In this reference frame, joint torques are the sums of vector cross products between the spatial positions of limb segments and their spatial accelerations and velocities. We simulated a model for a 3 joint arm in a two-dimensional plane and compared the results of the model with recordings from neurons in the motor cortex during similar movements. Comparisons between the population vector of the model and the population vector from the cortex revealed a close correspondence in the distribution of preferred directions, dependence on the workspace, and the rotation of the population vector. Finally we show how vector products can be used directly to compute the muscle tensions for the agonist and antagonist muscles in an arm. This computational framework for the function of the motor cortex greatly simplifies the control of multijoint limbs and can be scaled up to control all of the muscles in the body.
Motor Control
In curved hand movements, the angular speed is proportional to ⅔ power of the curvature. Several models have been proposed to explain the origin of this power law from optimality principles. However, we recently found that this law only holds for movement paths that have quickly changing curvature (such as ellipses), but not for paths with slowly changing curvature, such as spirals. We have developed a new model for smooth arm movements and have shown that it agrees with the results for spirals and makes many more predictions that we are in the process of testing (Huh 2011). The new model integrates the dopamine reward system (Montague, Dayan et al. 1996) with motor control and gives rise to a version of optimal stochastic control with an infinite horizon; that is, a fixed spatial target rather than a fixed time for the arm movement. This new model makes testable predictions that should inspire new experiments.
Sleep
Sleep spindles are bursts of 11-15 Hz oscillations in the EEG during non-REM sleep. Previous models of spindles in cats focused on the thalamus, which is capable of generating spindles in the absence of the cortex (Destexhe, Bal et al. 1996). In collaboration with Igor Timofeev at Laval, we developed a model of interactions between the cortex and the thalamus that better explains experimental data on the initiation, duration and termination of sleep spindles (Bonjean in press). We recently extended the model to humans sleep spindles (Fig. 3), which are highly synchronous across the scalp when measured with EEG, but have low spatial coherence and exhibit low correlation with EEG signals when simultaneously measured with MEG. We used a computational model to explore the hypothesis that MEG was picking up the deeper core system and the EEG was most sensitive to the superficial matrix system (Bonjean submitted). The model included interactions between the two systems. We collaborated with Syd Cash at MGH who recorded directly from the cortex of epilepsy patients with laminar electrodes and confirmed the predictions of the model.
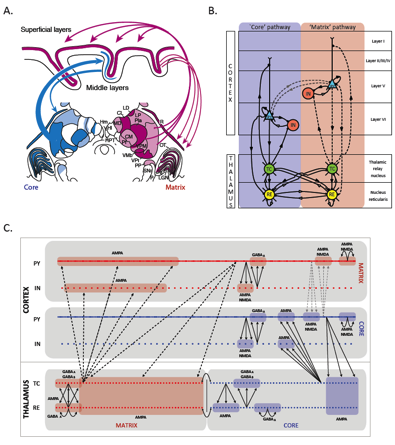
Fig. 1 Thalamocortical model of sleep spindles. (A) Thalamic inputs from the core system (blue) project to layer 4 in cortex, and the laminar system (red) projects to layer 1. (B) Simplified model of the two systems. (C) Detailed Hodgkin-Huxley model of interactions between the matrix and core systems (Bonjean submitted).
Science and Engineering of Learning
Terry Sejnowski was the senior author on a Science article that explored the implications of advances in our knowledge of biological and machine learning for educational practice (Meltzoff, Kuhl et al. 2009). The goal is to improve the educational outcomes of children by making them better learners.
References:
- Alexander, A. S., Kane, N.R., Mozer, M.C., Sejnowski, T.J., Chiba, A.A. (2010). " Rodents effectively learn statistics of hidden food rewards in a novel search task,." Society for Neuroscience Abstracts.
- Bazhenov, M., M. Stopfer, et al. (2001). "Model of cellular and network mechanisms for odor-evoked temporal patterning in the locust antennal lobe." Neuron 30(2): 569-581.
- Bazhenov, M., M. Stopfer, et al. (2001). "Model of transient oscillatory synchronization in the locust antennal lobe." Neuron 30: 553-567.
- Bonjean, M., Baker, T., Bazhenov, M., Cash, S., Halgren, E., Sejnowski, T. J. (submitted). "Interactions between core and matrix thalamocortical projections in human sleep spindle synchronization." Neuron.
- Bonjean, M., Baker, T., Lemieux, M., Timofeev, I., Sejnowski, T. J., Bazhenov, M. (in press). "Corticothalmamic Feedback Controls Sleep Spindle Duration In Vivo." Journal of Neuroscience.
- Chukoskie, L., Schwartz, O., Sejnowski, T.J., Dayan, P., Krauzlis, R. J. (2005). "Deciding where to look when there's not much to see." Society for Neuroscience Abstracts.
- Destexhe, A., T. Bal, et al. (1996). "Ionic mechanisms underlying synchronized oscillations and propagating waves in a model of ferret thalamic slices." Journal of neurophysiology 76(3): 2049-2070.
- Eagleman, D. M. and T. J. Sejnowski (2000). "Motion integration and postdiction in visual awareness." Science 287(5460): 2036-2038.
- Eagleman, D. M. and T. J. Sejnowski (2007). "Motion signals bias localization judgments: a unified explanation for the flash-lag, flash-drag, flash-jump, and Frohlich illusions." Journal of vision 7(4): 3.
- Filimon, F., Nelson, J. D., SEjnowski, T.J, Sereno, M. I., Cottrell, G. W. (2011). "Expected value of information overlaps with reward circuits in humans." Society for Neuroscience Abstracts.
- Finelli, L. A., S. Haney, et al. (2008). "Synaptic learning rules and sparse coding in a model sensory system." PLoS computational biology 4(4): e1000062.
- Huh, D. S., T. J. , Computational and Systems Neuroscience (2011). "Two-Third Power Law for Curved Movements Provides a Strict Constraint on Optimal Control Models." Cosyne Abstract.
- Meltzoff, A. N., P. K. Kuhl, et al. (2009). "Foundations for a new science of learning." Science 325(5938): 284-288.
- Mishra, J., J. M. Fellous, et al. (2006). "Selective attention through phase relationship of excitatory and inhibitory input synchrony in a model cortical neuron." Neural networks : the official journal of the International Neural Network Society 19(9): 1329-1346.
- Moldakarimov, S., M. Bazhenov, et al. (2010). "Representation sharpening can explain perceptual priming." Neural computation 22(5): 1312-1332.
- Montague, P. R., P. Dayan, et al. (1996). "A framework for mesencephalic dopamine systems based on predictive Hebbian learning." The Journal of neuroscience : the official journal of the Society for Neuroscience 16(5): 1936-1947.
- Nelson, J. D., C. R. McKenzie, et al. (2010). "Experience matters: information acquisition optimizes probability gain." Psychological science : a journal of the American Psychological Society / APS 21(7): 960-969.
- Peterson, D. A., D. T. Lotz, et al. (2011). "Choice modulates the neural dynamics of prediction error processing during rewarded learning." NeuroImage 54(2): 1385-1394.
- Schwartz, O., T. J. Sejnowski, et al. (2006). "Soft mixer assignment in a hierarchical generative model of natural scene statistics." Neural computation 18(11): 2680-2718.
- Schwartz, O., T. J. Sejnowski, et al. (2009). "Perceptual organization in the tilt illusion." Journal of vision 9(4): 19 11-20.
- Tanaka, H., Krakauer, J. W., Sejnowski, T. J. (in press). "The Implications for Generalization When Motor Adaptation is Multi-rate." Neural Computation.
- Tanaka, H., T. J. Sejnowski, et al. (2009). "Adaptation to visuomotor rotation through interaction between posterior parietal and motor cortical areas." Journal of Neurophysiology 102(5): 2921-2932.
- Tanaka, H., Sejnowski, T. J. (Submitted). "Motor cortex can compute muscle dynamics in Cartesian spatial coordinates." Neuron
