CNL Research 2016
Terrence J. Sejnowski
Research Goals
The research goal of my laboratory is to develop computational models of the nervous system that integrate experimental results across levels of investigation. The three major focuses of research are on 1) biophysical models of synapses; 2) dynamics of processing in neural circuits, and 3) learning and memory in neural systems.
My h-index is 131 and I have 93,255 citations on Google Scholar as of March 23, 2016:
https://scholar.google.ca/citations?user=m1qAiOUAAAAJ&hl=en
How Are Memories Formed and
Consolidated?
Despite great advances in our knowledge of the
mechanisms underlying synaptic plasticity, there are gaps in our understanding of
learning and memory between the cellular and systems levels. In the last 5 years my lab has made 3 advances
at the synaptic, circuit and systems levels that are beginning to fill in some
of these gaps.
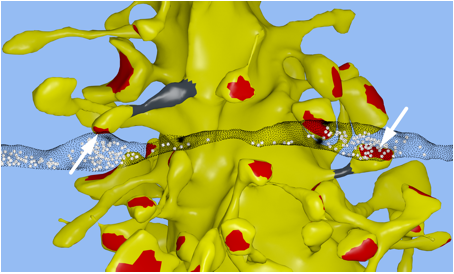
Synapses: In collaboration with Kristen
Harris and Chandra Bajaj at the University of Texas at Austin, we reconstructed
a 6x6x5 µm 3 piece of the rat
CA1 hippocampal neuropil from electron microscopic (EM) sections. Our goal was
to achieve the highest fidelity geometric reconstruction possible, including a
restoration of the extracellular space, which is lost during dehydration of the
tissue [1, 2]. For a video of the reconstruction see: http://www.youtube.com/watch?v=FZT6c0V8fW4 Our reconstruction is accurate at the nanometer scale to keep track of
biochemical interactions in nanoscale compartments, whereas most microconnectomic
reconstructions only achieve a wiring diagram.
Nanoconnectomic upper bound on the variability of synaptic plasticity[3]
The release of neurotransmitter at excitatory synapses in the cerebral cortex and the hippocampus is probabilistic and because synaptic plasticity depends on the history of presynaptic and postsynaptic activity, the amount of information that can be stored at a synapse in the form of a retrievable synaptic efficacy is limited. The trial-by-trial variability may, however, mask a more reliable intrinsic precision. We approached this question by taking advantage of a previously established correlation between the size of the spine head on pyramidal dendrites and the efficacy of a synapse, which allowed us to estimate the variability of synaptic plasticity.
In our EM reconstruction of hippocampal neuropil we found 10 single axons making two or more synaptic contacts onto the same dendrites, having shared histories of presynaptic and postsynaptic activity (Fig. 1). The postsynaptic spine heads, but not the spine necks, of these pairs were nearly identical in size, for the small as well as the large spine heads. This finding was confirmed in two other rats. This unexpectedly low variability allows 26 different values of the synaptic strength to be distinguished, corresponding to 4.7 bits of information, across synapses that vary in size over a factor of 60. This is an order of magnitude greater precision than previous estimates and requires postsynaptic averaging over minutes of activity because of stochastic variability. This raises two interesting questions: How is this precision achieved at the molecular level and why is the precision so high if most release probabilities are so low?
Circuits: Protein synthesis is
necessary to form long-term memories and mRNA and ribosomes are abundant within
dendrites regulate the long-term anatomical changes of synaptic efficacy. The time scale for these changes is
hours, much longer than the millisecond time scale of electrical signals. Most
neural network models ignore these longer time scales. We asked whether new computational
principles might emerge from these long time scales.
Selective memory
generalization by spatial patterning of protein synthesis [4]
We developed a computational model of synaptic plasticity that included synaptic tagging and capture, in which a weakly potentiated synapse can be "rescued" by a nearby synapse that is strongly potentiated within an hour. Spatially patterned protein synthesis within dendrites can enable selective consolidation of some memories but forgetting of others, even for simultaneous events that are represented by the same neural population. Key factors regulating selectivity include the functional clustering of synapses on dendrites and the sparsity and overlap of neural activity patterns at the circuit level. Based on these findings we proposed a novel two-step model for selective memory generalization during rapid eye movement (REM) and slow-wave sleep. Experimental confirmation for the branch-specific formation of dendritic spines during sleep, appeared shortly after it was published. ("Sleep promotes branch-specific formation of dendritic spines," Yang et al., Science 344, 1173-1178, 2014).
Systems: Sleep, which consumes about a
third of our lives, is thought to have a critical role in memory processes. The
effects of sleep on memory consolidation were first observed in behavioral
studies where there was an improvement in the performance for various memory
tasks after sleep compared to a similar awake period. This improvement has been
observed in declarative, procedural and emotional memory tasks. Although behavioral studies have shown a
significant effect of sleep on memories, the neural mechanisms are not known. During
slow-wave sleep, the cortex is decoupled from external inputs and can be
devoted to consolidating previously acquired labile memories into stable
memories. Recently, memory replay has been demonstrated during sleep, and
associated with characteristic oscillations, giving rise to the hypothesis that
these may form the critical neural substrate for memory consolidation.
Large-scale
spatiotemporal structure of thalamocortical spindle oscillations [5-8]
Electrocorticographic (ECoG) recordings from the surface of the cortex
in humans are used to locate the focus of seizures in epilepsy patients. In collaboration with Syd Cash at the
Massachusetts General Hospital in Boston, we have analyzed human ECoG
recordings during sleep. We were
particularly interested in sleep spindles that occur during stage 2 of non-REM
sleep. Spindles are 10-14 Hz
repetitive bursts of activity that originate in the thalamus last for 1-2
seconds and entrain the cortex.
Sleep spindles are known to be critical for sleep-dependent
consolidation of long-term memory. My
laboratory has developed detailed biophysical models of the ionic mechanisms
underlying the generation and termination of sleep spindles [5, 9].
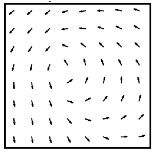

Figure 2. ECoG electrode array (left) and average vector field for phase change (right) across the array averaged over 1225 spindles in a single subject.
Spindle activity was thought to occur synchronously across the cortex. We developed new analysis methods to
track the phase of traveling waves in the cortex and found that that cortical
spindles form repeating circular wave-like patterns across the entire cortex
(Fig. 2) [6]. The short-range association fibers could
support this global pattern neuronal activity, with time delays of tens of
milliseconds between neighboring regions, a timescale highly relevant for
spike-time dependent plasticity (STDP): If spindles were synchronous
across the cortex, then spikes from nearby regions of cortex would arrive after
a delay of 5-10 ms, within the range for long-term depression from STDP. But with a circular wave the delayed
spikes from one area would arrive at about the same time because of the phase
delay in the traveling wave. STDP
is effective when repeated at 10-20 Hz,
in the range of spindle frequencies. Spindle oscillations could therefore serve
as a system for globally organizing sleep-dependent memory consolidation.
How Are Cortical States Regulated?
In addition to the feedforward flow of sensory information from the
periphery up through the cortical hierarchy, there is also active top-down
attentional control, which is characterized by an increase in signal-to-noise
ratio for neurons representing the attended stimulus. This is accompanied by a decrease in power
measured in local field potentials at low frequencies (below 10 Hz) and an increase
in power in the higher gamma frequencies (30 - 80 Hz). The field potential is a measure of the
average synaptic and subthreshold activity in nearby cells.
Inhibitory Regulation of Cortical States [10-12]
Fast-spiking parvalbumin-positive (PV) inhibitory interneurons constitute 5 percent of the neurons in the cerebral cortex and make multiple synapses around the soma of pyramidal cells; for this reason, they are called "basket" cells. These interneurons receive strong excitatory inputs from the more numerous pyramidal cells, which they reciprocally inhibit, and are involved in generating gamma oscillations. We developed a network model that explains how the reciprocal interactions between pyramidal neurons and basket cells could give rise to gamma oscillations and why the frequency and power in the visual cortex can be modulated as a function of stimulus size and contrast [10-12]. One of the intriguing predictions that came out of the model is that input to a column of neurons from neighboring columns can both decrease the firing rates of neurons, called surround suppression, and improve the precision of spike timing in pyramidal neurons, shifting the neural code from a rate code to a spike timing code.
Influence of
astrocytes on gamma oscillations [13]
Cortical neurons and synapses are surrounded by glial cells called astrocytes, which are well placed to support communication between neurons [14]. However, the functions typically attributed to astrocytes are significantly slower than the timescale of synaptic transmission between neurons. Consequently, it has been assumed that astrocytes do not have a major role in modulating fast neural network dynamics known to accompany cognitive behavior. In collaboration with Steve Heinemann, whose lab created a triple transgenic mouse in which vesicular release from astrocytes can be reversibly blocked, my lab found that astrocytes are necessary to maintain functional gamma oscillations both in vitro and in awake-behaving animals. Furthermore, vesicular release is needed for novel object recognition behavior suggesting an unexpected role for astrocytes in neural information processing and cognition [13].
Downregulation
of GAD67 in a mouse model for psychosis [15-22]
The pathophysiology of
schizophrenia is complex and involves many different cortical and subcortical
systems. The slow development of fast-spiking PV-interneurons, although
essential for shaping neuronal circuits during postnatal brain development,
increases their vulnerability to insults that can permanently affect their
maturational process and lead to cortical dysfunction and perhaps schizophrenia
in adulthood. Reduced expression of GAD67 in fast-spiking PV-interneurons (the
main isoform synthesizing GABA in the brain) is one of the most replicated
findings in postmortem brain studies of schizophrenia. We are exploring an experimental rodent
model of psychosis that can be induced by subanesthetic injections of NMDA
receptor blockers such as ketamine or phencyclidine (PCP) [22].
In humans, ketamine is taken as a party drug that induces temporary hallucinations
and other psychotic symptoms. In
adult mice, ketamine injection leads to the temporary downregulation of GAD67
in basket cells, but my lab has shown that this becomes permanent if the
injections occur during the second postnatal week, when the basket cells are
maturing [22].
Using slice recordings from mouse prefrontal cortex, we found that ketamine
treatment reduces the power in the gamma range [21]
as previously reported in schizophrenia patients. We explore the impact of downregulating
the PV-interneurons on the function of the cortex in neural circuit models and
have shown that a reduction in both GAD67 and fast-spiking PV expression may
contribute to the decrease in gamma power [17, 20].
Methylation
of DNA during cortical development [23-26]
In the search for a possible substrate for gene dysregulation in the ketamine model, we discovered that DNA methylation inhibitors blocked the effects of ketamine on the inhibitory interneurons and behavioral effects
[27]. In collaboration with HHMI Investigator Joseph Ecker at the Salk Institute, my laboratory carried out a genome-wide, base-resolution DNA methylation profile of cortical neurons and glial cells from fetus to old age in mice and humans
[24] .
We discovered that unlike the DNA in glial cells and mature cells in other body organs, which are exclusively methylated on CpG sequences, the DNA of neurons is also methylated on cytosines that are not adjacent to guanine bases, and that this non-CpG methylation starts at birth, rises in tandem with synaptogenesis and reaches a peak in early adulthood. My lab was responsible for the neuroscience and bioinformatics in this study. In collaboration with HHMI Investigator Jeremy Nathans we undertook a similar analysis of DNA methylation of the PV interneurons, which is the subpopulation affected by ketamine treatment [25]Feedback
projections to the olfactory bulb [28-30]
The olfactory bulb receives feedback projections from a wide range of areas. Using the retrograde viral tracers developed by Ed Callaway, we reconstructed all of these feedback neurons and were surprised to find a substantial projection from the hippocampus to the granule cell layer of the olfactory bulb [28, 29]. This may explain the strong contextual influence on olfactory processing in the bulb [30].
How Are Sensorimotor Interactions Organized?
In addition to computational modeling of synapses and circuits, my lab
also has developed new theoretical approaches to understanding natural images
and the regularities that are observed in sensorimotor coordination. Theory provides a framework for thinking
about the computational problems that the brain faces and provides constraints
on neural models.
Natural
images [31-36]
Natural outdoor scenes have spatial structure over a wide range of
spatial scales. My lab has analyzed
the statistics of natural scenes on a hierarchy of scales and found evidence of
a sharp phase transition at a particular intensity. At the phase transition there are
long-range correlations across the image that may be the origin of scale
invariance that has been observed in natural images [31, 33-35].
Learning
Where to Look [37-40]
Humans forage for information by foveating visual targets and can rapidly redirect gaze in a context and task-appropriate manner. We asked subjects to search for a target whose location was drawn stochastically on each trial from a fixed prior distribution. The target was invisible on a blank screen, and the participants were rewarded when they fixated the hidden target location. In just a few trials, participants rapidly found the hidden targets by looking near previously rewarded locations and avoiding previously unrewarded locations. A reinforcement-learning (RL) model based on the responses of dopamine neurons in the brain could reproduce the learning curve and sensitivity to recent experience. The asymptotic performance of both the subjects and the RL model approached optimal performance characterized by an ideal-observer theory [37]. The brain can efficiently learn how to gather information from the world appropriate for the current context and task at hand [40].
Power Laws for Curved Hand Movements [41, 42]
The speed of curved hand movements around ellipses tends to scale
inversely with the curvature to the _1/3 power. We showed that there is a set
of basis shapes which have power laws with exponents ranging from 0 to -2/3.
More general movements exhibited mixtures of power laws. The speed of arbitrary
doodling movements with a broad spectrum of frequencies could also be predicted
from the curvature with high accuracy [41]. The
overall speed is regulated by a conserved quantity, which may be related to
tonic levels of neuromodulators [42].
Sensorimotor Coordination [43-45]
Although many neurons in the primary motor cortex (M1) project directly
to the spinal cord, how they control movements is not yet understood. Some M1 neurons
represent intrinsic dynamical variables such as muscle tensions, whereas other
neurons code for extrinsic kinematic variables such as movement trajectories.
These observations can be reconciled if the motor cortex uses spatial reference
frames in which the equations of motion governing reaching simplify. The
performance of human-machine interfaces might be improved by computing joint
torques from neural activity in M1 using a spatial reference frame.
Delay Differential Analysis (DDA)[46-52]
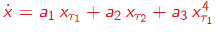
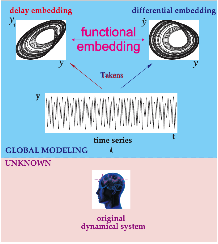
Figure 4. Delay Differential Analysis. The time series is generated by an unknown dynamical system (bottom). The time series can be embedded in recurrence plots (above). The nonlinear DDE (red) bridges these two plots where ti are time delays and ai are fitted coefficients.
My lab is collaborating with Syd Cash at MGH and Eric Halgren at UCSD on memory consolidation in humans. We are looking for neural correlates in the cortex for replay during sleep following a learning experience. Preliminary results are promising: The ECoG recordings during sleep after learning are more similar to the patterns during the encoding phase of the learning than they are to the previous sleep episode. We plan to analyze sleep spindles, which are triggered by the hippocampus during stage 2 intermediate non–REM sleep preceding slow wave sleep, where we see evidence for replay.
We have used DDA to analyze ECoG from seizing human brains [56]. This new analysis method holds great promise for predicting seizures. DDA efficiently discriminates between different neurologic states and epileptic events from the raw ECoG data. The global and local dynamics can be delineated with DDA to differentiate electrographic and electroclinical seizures while also providing insight into a highly localized seizure onset and diffuse seizure termination. Seizures are quite diverse and we will need to study more patients to see the range of seizures that can occur. We are also collaborating with Igor Timofeev at Laval University in Quebec who works on animal models of epilepsy to explore the hypothesis that dysregulation of homeostatic synaptic plasticity following brain trauma may be involved in epileptogenesis [83, 84]
We are collaborating with Greg Light in the Department of Psychiatry at UCSD to analyze EEG recordings from schizophrenia patients using DDA in order to develop a biomarker for the early detection of schizophrenia. We have analyzed a large EEG database of recordings from a mismatch negativity task (Consortium on the Genetics of Schizophrenia (COGS-2): 877 SZ patients and 753 non-psychiatric comparison subjects). In a preliminary study we detected 6 dissociable subgroups within the dataset, including controls who clustered with some schizophrenia patients [55].
BRAIN Initiative [58-62]
Several influential publications grew out of the 14 month long Working Group of the Advisory Committee to the Director of NIH for the BRAIN Initiative: The final report, BRAIN 2025 [58], a summary [59], and an expanded version of the section on big data [62].
References
[1] J. Edwards, E. Daniel, J. Kinney, T. Bartol, T. Sejnowski, D. Johnston, et al., "VolRoverN: enhancing surface and volumetric reconstruction for realistic dynamical simulation of cellular and subcellular function," Neuroinformatics, vol. 12, pp. 277-89, Apr 2014.
[2] J. P. Kinney, J. Spacek, T. M. Bartol, C. L. Bajaj, K. M. Harris, and T. J. Sejnowski, "Extracellular sheets and tunnels modulate glutamate diffusion in hippocampal neuropil," J Comp Neurol, vol. 521, pp. 448-64, Feb 1 2013.
[3] T. M. Bartol, C. Bromer, J. Kinney, M. A. Chirillo, J. N. Bourne, K. M. Harris, et al., "Nanoconnectomic upper bound on the variability of synaptic plasticity," Elife, vol. 4, 2015.
[4] C. O'Donnell and T. J. Sejnowski, "Selective memory generalization by spatial patterning of protein synthesis," Neuron, vol. 82, pp. 398-412, Apr 16 2014.
[5] M. Bonjean, T. Baker, M. Bazhenov, S. Cash, E. Halgren, and T. Sejnowski, "Interactions between core and matrix thalamocortical projections in human sleep spindle synchronization," J Neurosci, vol. 32, pp. 5250-63, Apr 11 2012.
[6] L. P. Muller, S. Koller, D. Cash, S. S. Halgren, E. Sejnowski, T. J. ,, "Large-scale spatiotemporal structure of spindle oscillations," Nature Neuroscience, submitted.
[7] H. Wei, M. Bonjean, H. M. Petry, T. J. Sejnowski, and M. E. Bickford, "Thalamic burst firing propensity: a comparison of the dorsal lateral geniculate and pulvinar nuclei in the tree shrew," J Neurosci, vol. 31, pp. 17287-99, Nov 23 2011.
[8] T. T. Dang-Vu, M. Bonjean, M. Schabus, M. Boly, A. Darsaud, M. Desseilles, et al., "Interplay between spontaneous and induced brain activity during human non-rapid eye movement sleep," Proc Natl Acad Sci U S A, vol. 108, pp. 15438-43, Sep 13 2011.
[9] M. Bonjean, T. Baker, M. Lemieux, I. Timofeev, T. Sejnowski, and M. Bazhenov, "Corticothalamic feedback controls sleep spindle duration in vivo," J Neurosci, vol. 31, pp. 9124-34, Jun 22 2011.
[10] M. P. Jadi and T. J. Sejnowski, "Regulating Cortical Oscillations in an Inhibition-Stabilized Network," Proc IEEE Inst Electr Electron Eng, vol. 102, Apr 21 2014.
[11] M. P. Jadi and T. J. Sejnowski, "Cortical oscillations arise from contextual interactions that regulate sparse coding," Proc Natl Acad Sci U S A, vol. 111, pp. 6780-5, May 6 2014.
[12] R. Veltz and T. J. Sejnowski, "Periodic Forcing of Inhibition-Stabilized Networks: Nonlinear Resonances and Phase-Amplitude Coupling," Neural Comput, vol. 27, pp. 2477-509, Dec 2015.
[13] H. S. Lee, A. Ghetti, A. Pinto-Duarte, X. Wang, G. Dziewczapolski, F. Galimi, et al., "Astrocytes contribute to gamma oscillations and recognition memory," Proc Natl Acad Sci U S A, vol. 111, pp. E3343-52, Aug 12 2014.
[14] R. D. Fields, A. Araque, H. Johansen-Berg, S. S. Lim, G. Lynch, K. A. Nave, et al., "Glial biology in learning and cognition," Neuroscientist, vol. 20, pp. 426-31, Oct 2014.
[15] S. A. Barnes, A. Pinto-Duarte, A. Kappe, A. Zembrzycki, A. Metzler, E. A. Mukamel, et al., "Disruption of mGluR5 in parvalbumin-positive interneurons induces core features of neurodevelopmental disorders," Mol Psychiatry, vol. 20, pp. 1161-72, Oct 2015.
[16] M. M. Behrens and T. J. Sejnowski, "Does schizophrenia arise from oxidative dysregulation of parvalbumin-interneurons in the developing cortex?," Neuropharmacology, vol. 57, pp. 193-200, Sep 2009.
[17] M. P. Jadi, M. Margarita Behrens, and T. J. Sejnowski, "Abnormal Gamma Oscillations in N-Methyl-D-Aspartate Receptor Hypofunction Models of Schizophrenia," Biol Psychiatry, Jul 17 2015.
[18] B. Ji, X. Wang, A. Pinto-Duarte, M. Kim, S. Caldwell, J. W. Young, et al., "Prolonged Ketamine Effects in Hypomorphic Mice: Mimicking Phenotypes of Schizophrenia," PLoS One, vol. 8, p. e66327, 2013.
[19] S. B. Powell, T. J. Sejnowski, and M. M. Behrens, "Behavioral and neurochemical consequences of cortical oxidative stress on parvalbumin-interneuron maturation in rodent models of schizophrenia," Neuropharmacology, vol. 62, pp. 1322-31, Mar 2012.
[20] V. Volman, M. M. Behrens, and T. J. Sejnowski, "Downregulation of parvalbumin at cortical GABA synapses reduces network gamma oscillatory activity," J Neurosci, vol. 31, pp. 18137-48, Dec 7 2011.
[21] X. Wang, A. Pinto-Duarte, M. Margarita Behrens, X. Zhou, and T. J. Sejnowski, "Characterization of spatio-temporal epidural event-related potentials for mouse models of psychiatric disorders," Sci Rep, vol. 5, p. 14964, 2015.
[22] X. Wang, A. Pinto-Duarte, T. J. Sejnowski, and M. M. Behrens, "How Nox2-containing NADPH oxidase affects cortical circuits in the NMDA receptor antagonist model of schizophrenia," Antioxid Redox Signal, vol. 18, pp. 1444-62, Apr 20 2013.
[23] A. Kundaje, W. Meuleman, J. Ernst, M. Bilenky, A. Yen, A. Heravi-Moussavi, et al., "Integrative analysis of 111 reference human epigenomes," Nature, vol. 518, pp. 317-30, Feb 19 2015.
[24] R. Lister, E. A. Mukamel, J. R. Nery, M. Urich, C. A. Puddifoot, N. D. Johnson, et al., "Global epigenomic reconfiguration during mammalian brain development," Science, vol. 341, p. 1237905, Aug 9 2013.
[25] A. Mo, E. A. Mukamel, F. P. Davis, C. Luo, G. L. Henry, S. Picard, et al., "Epigenomic Signatures of Neuronal Diversity in the Mammalian Brain," Neuron, vol. 86, pp. 1369-84, Jun 17 2015.
[26] M. D. Schultz, Y. He, J. W. Whitaker, M. Hariharan, E. A. Mukamel, D. Leung, et al., "Human body epigenome maps reveal noncanonical DNA methylation variation," Nature, vol. 523, pp. 212-6, Jul 9 2015.
[27] M. Behrens, Hasenstaub, A., Sejnowski, T.J., "A role for DNA methylation in the NMDA receptor antagonist-mediated loss of phenotype of parvalbumin-positive fast-spiking interneurons," Society for Neuroscience Abstracts, 2010.
[28] K. O. Padmanabhan, F. Tarabrina, A. Kizer, E. Callaway, E. M. Gage, F. H. and Sejnowski, T. J. , "Diverse representations of olfactory information in centrifugal feedback projections," J. Neuroscience, (submitted).
[29] F. T. Padmanabhan. K. Osakada, A. Kizer, E. Callaway, E. M. Gage, F. H. Sejnowski, T. J. , , "CA1 hippocampal inputs to the main olfactory bulb revealed through whole brain circuit-mapping," eLife, (submitted).
[30] D. H. Gire, D. Restrepo, T. J. Sejnowski, C. Greer, J. A. De Carlos, and L. Lopez-Mascaraque, "Temporal processing in the olfactory system: can we see a smell?," Neuron, vol. 78, pp. 416-32, May 8 2013.
[31] S. Saremi, Sejnowski, T. J. , "Correlated percolation, fractal structures, and scale-invariant distribution of clusters in natural images," IEEE Transactions on Pattern Analysis and Machine Intelligence, (in press).
[32] S. Saremi, Sejnowski, T. J. , "The Wilson Machine for Image Modeling," arXiv, vol. 1510.07740v1, 2015.
[33] S. Saremi and T. Sejnowski, "Correlated percolation, fractal structures, and scale-invariant distribution of clusters in natural images," IEEE Trans Pattern Anal Mach Intell, Sep 23 2015.
[34] S. Saremi and T. J. Sejnowski, "On criticality in high-dimensional data," Neural Comput, vol. 26, pp. 1329-39, Jul 2014.
[35] S. Saremi and T. J. Sejnowski, "Hierarchical model of natural images and the origin of scale invariance," Proc Natl Acad Sci U S A, vol. 110, pp. 3071-6, Feb 19 2013.
[36] S. Saremi, T. J. Sejnowski, and T. O. Sharpee, "Double-gabor filters are independent components of small translation-invariant image patches," Neural Comput, vol. 25, pp. 922-39, Apr 2013.
[37] L. Chukoskie, J. Snider, M. C. Mozer, R. J. Krauzlis, and T. J. Sejnowski, "Learning where to look for a hidden target," Proc Natl Acad Sci U S A, vol. 110 Suppl 2, pp. 10438-45, Jun 18 2013.
[38] D. A. Peterson, C. Elliott, D. D. Song, S. Makeig, T. J. Sejnowski, and H. Poizner, "Probabilistic reversal learning is impaired in Parkinson's disease," Neuroscience, vol. 163, pp. 1092-101, Nov 10 2009.
[39] D. A. Peterson, D. T. Lotz, E. Halgren, T. J. Sejnowski, and H. Poizner, "Choice modulates the neural dynamics of prediction error processing during rewarded learning," Neuroimage, vol. 54, pp. 1385-94, Jan 15 2011.
[40] T. J. Sejnowski, H. Poizner, G. Lynch, S. Gepshtein, and R. J. Greenspan, "Prospective Optimization," Proc IEEE Inst Electr Electron Eng, vol. 102, May 2014.
[41] D. Huh and T. J. Sejnowski, "Spectrum of power laws for curved hand movements," Proc Natl Acad Sci U S A, vol. 112, pp. E3950-8, Jul 21 2015.
[42] D. S. Huh, T. J. , "Drive is Conserved for Self-paced Movements," Proceedings of the National Academy of Sciences, USA, (submitted).
[43] H. Tanaka, J. W. Krakauer, and T. J. Sejnowski, "Generalization and multirate models of motor adaptation," Neural Comput, vol. 24, pp. 939-66, Apr 2012.
[44] H. Tanaka and T. J. Sejnowski, "Motor adaptation and generalization of reaching movements using motor primitives based on spatial coordinates," J Neurophysiol, vol. 113, pp. 1217-33, Feb 15 2015.
[45] H. Tanaka and T. J. Sejnowski, "Computing reaching dynamics in motor cortex with Cartesian spatial coordinates," J Neurophysiol, vol. 109, pp. 1182-201, Feb 2013.
[46] C. Lainscsek, M. E. Hernandez, H. Poizner, and T. J. Sejnowski, "Delay differential analysis of electroencephalographic data," Neural Comput, vol. 27, pp. 615-27, Mar 2015.
[47] C. Lainscsek, M. E. Hernandez, J. Weyhenmeyer, T. J. Sejnowski, and H. Poizner, "Non-linear dynamical analysis of EEG time series distinguishes patients with Parkinson's disease from healthy individuals," Front Neurol, vol. 4, p. 200, 2013.
[48] C. Lainscsek and T. J. Sejnowski, "Delay differential analysis of time series," Neural Comput, vol. 27, pp. 594-614, Mar 2015.
[49] C. Lainscsek and T. J. Sejnowski, "Electrocardiogram classification using delay differential equations," Chaos, vol. 23, p. 023132, Jun 2013.
[50] C. Lainscsek, J. Weyhenmeyer, M. E. Hernandez, H. Poizner, and T. J. Sejnowski, "Non-linear dynamical classification of short time series of the rossler system in high noise regimes," Front Neurol, vol. 4, p. 182, 2013.
[51] C. Lainscsek, J. Weyhenmeyer, T. J. Sejnowski, and C. Letellier, "Discovering independent parameters in complex dynamical systems," Chaos Solitons Fractals, vol. 76, pp. 182-189, Jul 2015.
[52] J. Weyhenmeyer, M. E. Hernandez, C. Lainscsek, T. J. Sejnowski, and H. Poizner, "Muscle artifacts in single trial EEG data distinguish patients with Parkinson's disease from healthy individuals," Conf Proc IEEE Eng Med Biol Soc, vol. 2014, pp. 3292-5, 2014.
[53] C. Lainscsek, Messager, V., Portman, A., Muir, J.-F., Sejnowski, T. J., Letellier. C., "Automatic Sleep Scoring from a Single Electrode Using Delay Differential Equations," in Dynamical Systems Theory and Applications, Lodz, Poland, 2013.
[54] A. L. Sampson, C.
Lainscsek, C., Cash, S. S., E., Halgren, E., Sejnowski, T. J., "Nonlinear
dynamical sleep spindle detection using delay differential analysis,," Society for Neuroscience Abstracts 2015.
[55] C. Lainscsek, Sampson, A., The COGS Investigators, Light, G. A., Sejnowski,T. J. , "Bringing order to the neurophysiological chaos underlying sensory processing dysfunction in schizophrenia," Society for Neuroscience Abstracts, 2015.
[56] J. L. Weyhenmeyer, C. Cash, S. S. Sejnowski, T. J. , "Delay differential analysis: a framework for the analysis of large-scale epileptic electrocorticography recordings," Society for Neuroscience Abstracts, 2015.
[57] W. Lin, Lainscsek, C., Krishnan, G. P,. Bazhenov, M., Mednick, S., Sejnowski, T. J. , "Nonlinear dynamical features for improving computational sleep models using Delay Differential Analysis," Society for Neuroscience Abstracts, 2015.
[58] C. I. Bargmann, Newsome, W. T., Anderson, D. J.,Brown, E. N., Deisseroth, K., Donoghue, J. P., MacLeish, P. R., Marder, E., Normann, R. A., Sanes, J. R., Schnitzer, M. J., Sejnowski, T. J., Tank, D. W., Tsien, R. Y., Ugurbil, K., , "BRAIN 2025: A Scientific Vision," http://www.braininitiative.nih.gov/2025/, 2014.
[59] L. A. Jorgenson, W. T. Newsome, D. J. Anderson, C. I. Bargmann, E. N. Brown, K. Deisseroth, et al., "The BRAIN Initiative: developing technology to catalyse neuroscience discovery," Philos Trans R Soc Lond B Biol Sci, vol. 370, May 19 2015.
[60] A. P. Alivisatos, A. M. Andrews, E. S. Boyden, M. Chun, G. M. Church, K. Deisseroth, et al., "Nanotools for neuroscience and brain activity mapping," ACS Nano, vol. 7, pp. 1850-66, Mar 26 2013.
[61] A. P. Alivisatos, M. Chun, G. M. Church, K. Deisseroth, J. P. Donoghue, R. J. Greenspan, et al., "Neuroscience. The brain activity map," Science, vol. 339, pp. 1284-5, Mar 15 2013.
[62] T. J. Sejnowski, P. S. Churchland, and J. A. Movshon, "Putting big data to good use in neuroscience," Nat Neurosci, vol. 17, pp. 1440-1, Nov 2014.
[63] M. B. Kennedy, "Signal-processing machines at the postsynaptic density," Science, vol. 290, pp. 750-754, 2000.
[64] T. M. Bartol, D. X. Keller, J. P. Kinney, C. L. Bajaj, K. M. Harris, T. J. Sejnowski, et al., "Computational reconstitution of spine calcium transients from individual proteins," Front Synaptic Neurosci, vol. 7, p. 17, 2015.
[65] T. M. S. Bartol, T. J. Nadkarni, S. Levine, H. , "Activity Dependent Modulation of Synaptic Transmission by Presynaptic Ryanodine Receptors: A dichotomy of Short-Term Depression and Facilitation," Society for Neuroscience Abstracts, 2013.
[66] C. Modchang, S. Nadkarni, T. M. Bartol, W. Triampo, T. J. Sejnowski, H. Levine, et al., "A comparison of deterministic and stochastic simulations of neuronal vesicle release models," Phys Biol, vol. 7, p. 026008, 2010.
[67] S. Nadkarni, T. M. Bartol, T. J. Sejnowski, and H. Levine, "Modelling vesicular release at hippocampal synapses," PLoS Comput Biol, vol. 6, p. e1000983, 2010.
[68] S. Nadkarni, T. M. Bartol, C. F. Stevens, T. J. Sejnowski, and H. Levine, "Short-term plasticity constrains spatial organization of a hippocampal presynaptic terminal," Proc Natl Acad Sci U S A, vol. 109, pp. 14657-62, Sep 4 2012.
[69] J. W. B. Garcia, T. M. Jr. Spencer, D. J. Sejnowski, T. J. , "An event-driven model of short-term presynaptic dynamics based on detailed molecular simulations with MCell," Society for Neuroscience Abstracts, 2015.
[70] J. M. Cortes, M. Desroches, S. Rodrigues, R. Veltz, M. A. Munoz, and T. J. Sejnowski, "Short-term synaptic plasticity in the deterministic Tsodyks-Markram model leads to unpredictable network dynamics," Proc Natl Acad Sci U S A, vol. 110, pp. 16610-5, Oct 8 2013.
[71] S. Rodrigues, M. Desroches, M. Krupa, J. M. Cortes, T. J. Sejnowski, and A. B. Ali, "Time-coded neurotransmitter release at excitatory and inhibitory synapses," Proc Natl Acad Sci U S A, Feb 8 2016.
[72] M. I. Stefan, T. M. Bartol, T. J. Sejnowski, and M. B. Kennedy, "Multi-state modeling of biomolecules," PLoS Comput Biol, vol. 10, p. e1003844, Sep 2014.
[73] K.-U. T. Pepke S., Mihalas S., Kennedy M. B. , "A dynamic model of interactions of Ca2+, calmodulin, and catalytic subunits of Ca2+/calmodulin-dependent protein kinase II.," PLoS Comput. Biol., vol. 6, p. e1000675, 2010.
[74] D. Vucinic and T. J. Sejnowski, "A compact multiphoton 3D imaging system for recording fast neuronal activity," PloS one, vol. 2, p. e699, 2007.
[75] B. M. Regner, D. M. Tartakovsky, and T. J. Sejnowski, "Identifying transport behavior of single-molecule trajectories," Biophys J, vol. 107, pp. 2345-51, Nov 18 2014.
[76] B. M. Regner, D. Vucinic, C. Domnisoru, T. M. Bartol, M. W. Hetzer, D. M. Tartakovsky, et al., "Anomalous diffusion of single particles in cytoplasm," Biophys J, vol. 104, pp. 1652-60, Apr 16 2013.
[77] A. Ruiz-Martinez, Bartol, T. M., Sejnowski, T. J. Tartakovsky, D. M. , "Efficient Multiscale Models of Polymer Assembly," Biophysical Journal,, (submitted).
[78] A. H. Williams, OÕDonnell, C., Sejnowski, T. J., and OÕLeary, T. , "Trafficking synaptic cargo involves tradeoffs in speed and precision," eLife (submitted).
[79] M. P. Jadi, Nandy, A. S., Sejnowski, T. J., Reynolds,J. H. , "Laminar organization of visually evoked gamma power in area V4," Society for Neuroscience Abstracts, 2015.
[80] S. Moldakarimov, M. Bazhenov, and T. J. Sejnowski, "Feedback stabilizes propagation of synchronous spiking in cortical neural networks," Proc Natl Acad Sci U S A, vol. 112, pp. 2545-50, Feb 24 2015.
[81] S. Moldakarimov, M. Bazhenov, and T. J. Sejnowski, "Top-down inputs enhance orientation selectivity in neurons of the primary visual cortex during perceptual learning," PLoS Comput Biol, vol. 10, p. e1003770, Aug 2014.
[82] S. Moldakarimov, Bazhenov, M., Feldman, D. E., Sejnowski, T. J., "Sparse rapidly propagating sensory encoding in rodent barrel cortex," Neuron, (submitted).
[83] O. C. Gonzalez, G. P. Krishnan, S. Chauvette, I. Timofeev, T. Sejnowski, and M. Bazhenov, "Modeling of Age-Dependent Epileptogenesis by Differential Homeostatic Synaptic Scaling," J Neurosci, vol. 35, pp. 13448-62, Sep 30 2015.
[84] I. Timofeev, T. J. Sejnowski, M. Bazhenov, S. Chauvette, and L. B. Grand, "Age dependency of trauma-induced neocortical epileptogenesis," Front Cell Neurosci, vol. 7, p. 154, 2013.
